
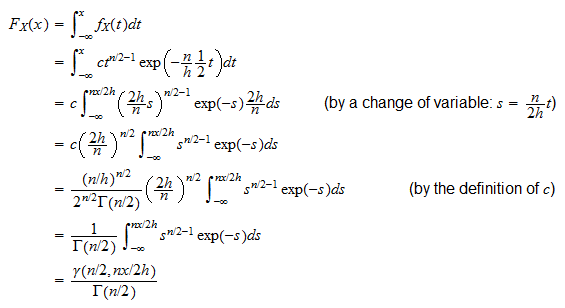
Here we have a family of conditional Poisson distributions where each one is conditional on the characteristics of the particular insured in question (a low risk insured has a low value and a high risk insured has a high value). The quantity varies from insured to insured but is supposed to follow a gamma distribution. Suppose that in a large pool of insureds, the annual claim frequency of an insured is a Poisson distribution with mean. There is an insurance interpretation of the Poisson-gamma mixture. In other words, the mixture of Poisson distributions with gamma mixing weights is a negative binomial distribution. What does this have to do with gamma distribution and Poisson distribution? When a conditional random variable has a Poisson distribution such that its mean is an unknown random quantity but follows a gamma distribution with parameters and as described in (1), the unconditional distribution for has a negative binomial distribution as described in (2). a random discrete variable modeling the number of occurrences of a type of random events. It is simply a counting distribution, i.e.
#Gamma cdf series
Then the distribution in (2) does not have a natural interpretation in terms of performing a series of independent Bernoulli trials. It only needs to be a positive real number. When is not an integer but is only a positive number, the binomial coefficient is calculated as follows:įor this new calculation to work, does not have to be a positive integer. Note that when is a positive integer, the binomial coefficient has the usual calculation. In this case, the quantity in (2) is the probability of having failures before the occurrence of the th success.
#Gamma cdf trial
Assume that the probability of a success in each trial is. Consider performing a series of independent trials where each trial has one of two distinct outcomes (called success or failure). If the parameter is a positive integer, then (2) has a nice interpretation in the context of a series of independent Bernoulli trials. The following is the probability function of this negative binomial distribution.

We can simply read off the information from the parameters and in the density function.įor a reason that will be given shortly, the parameters and in (1) gives a negative binomial distribution. Baked into this gamma probability density function are two pieces of information about the Poisson distribution. This density function describes how the potential gamma observations distribute across the positive x-axis. The numbers and, both positive, are fixed constants and are the parameters of the distribution. The following is the probability density function of the gamma distribution.

This post discusses the connections of the gamma distribution with Poisson distribution. The gamma distribution is important in many statistical applications.


 0 kommentar(er)
0 kommentar(er)
